考研信息
院校招生
考研备考
考研资料
考研复试
考研调剂
来源:研线网 责任编辑:superadmin 时间:2021-07-25
在考研数学中,线性方程组是线性代数的两大核心之一,也是一个非常重要的考点,在每年的考研数学中,线性方程组方面的内容往往以一个大题的形式出现,占11分,但2015年即数一、数二和数三只一个小题考到了非齐次线性方程组有无穷多解的判定问题。因此,今年的线性代数题目的难度下降了很多。
本章的常考题型有:
第一,齐次线性方程组有无零解和非齐次线性方程组是否有解的判定。对于齐次线性方程组,当方程组的方程个数和未知量的个数不等时,可以按照系数矩阵的秩和未知量个数的大小关系来判定,还可以利用系数矩阵的列向量组是否相关来判定;当方程组的方程个数和未知量个数相同时,可以利用系数行列式与零的大小关系来判定,还可以利用系数矩阵有无零特征值来判定;对于非齐次线性方程组,可以利用系数矩阵的秩和增广矩阵的秩是否相等即有关矛盾方程来判定,还可以从一个向量可否由一向量组线性表出来判定;当方程个数和未知量个数相等时,可以利用系数行列式是否为零来判定非齐次线性方程组的唯一解情况;2015年数一、数二和数三的一个小题就是利用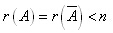 和系数行列式为0来判定非齐次线性方程组有无穷多解的。
和系数行列式为0来判定非齐次线性方程组有无穷多解的。
第二,齐次线性方程组的非零解的结构和非齐次线性方程组解的的无穷多解的结构问题。如果齐次线性方程组有无穷多个非零解时,其通解是由其基础解系来表示的;如果非齐次线性方程组有无穷多解时,其通解是由对应的齐次线性方程组和通解加本身一个特解所构成;
第三,齐次线性方程组基础解系的求解与证明。利用系数矩阵的极大线性无关组的内容进行分析;
第四,齐次(非齐次)线性方程组的求解(含对参数取值的讨论)。如果方程组的方程个数和未知量个数不相等时,只能对其系数矩阵或增广矩阵进行初等行变换,化为阶梯形矩阵来进行讨论;如果方程组的方程个数和未知量个数相同时,初等行变换和行列式可以结合起来一起进行分析和讨论

扫码添加获取各院校录取名单

扫码添加研线老师,打牢基础
2024考研备考择校指导
考研信息
院校招生
考研备考
考研资料
考研复试
考研调剂
择校蓝皮书